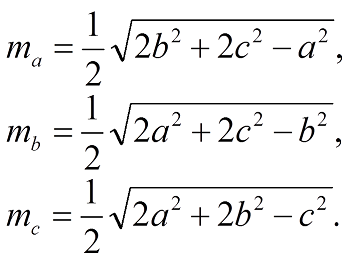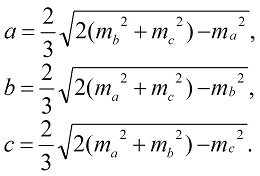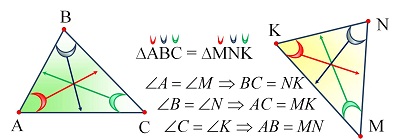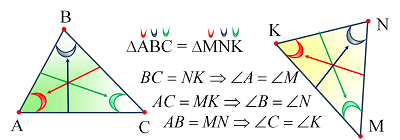Шпаргалка-запоминалка Планиметрия Треугольники (1 часть) |
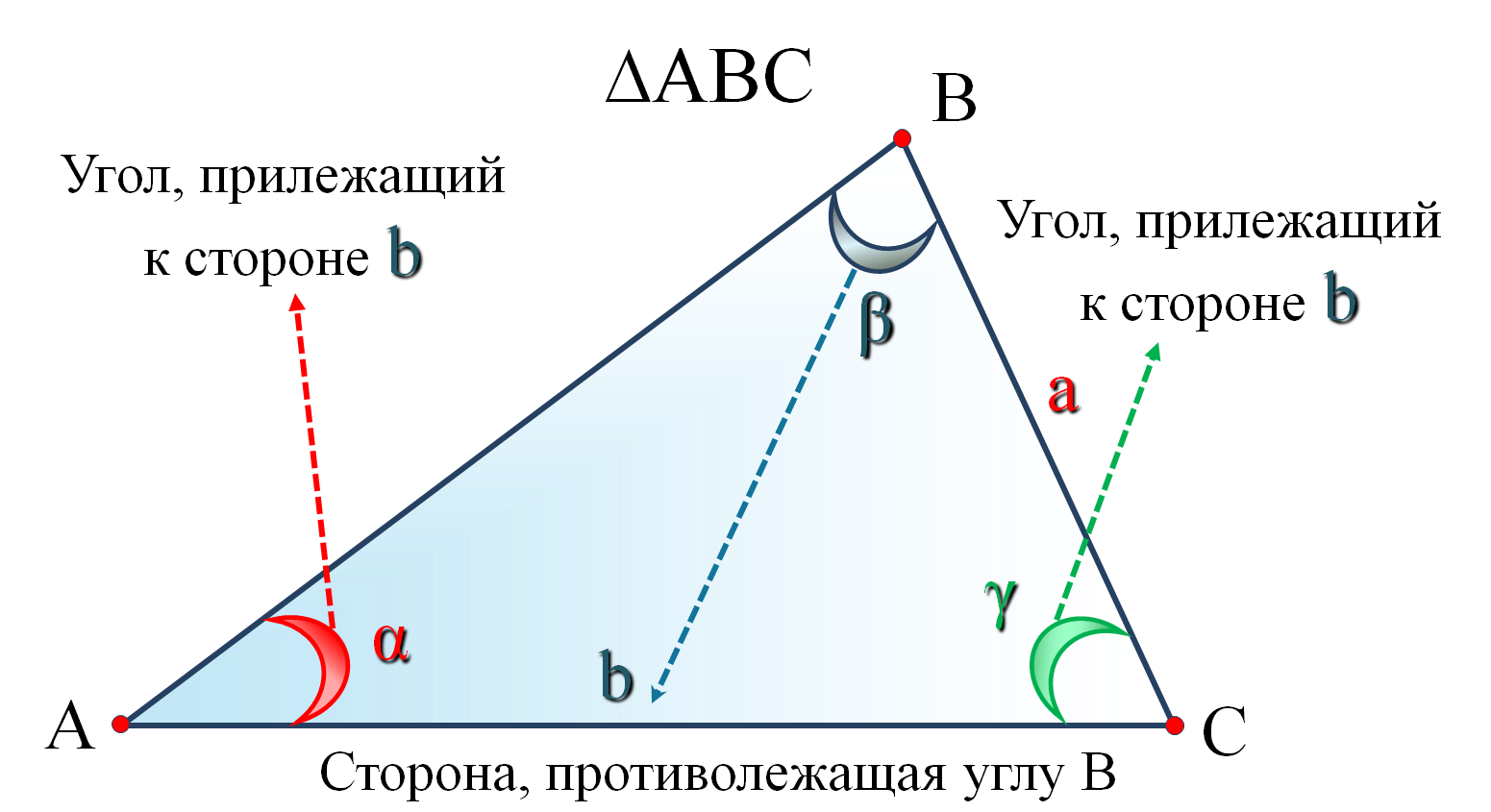
Опорные дидактические единицы: треугольник; вершины; стороны; сторона, противолежащая углу; угол, противолежащий стороне; угол, прилежащей к стороне; сторона, прилежащаяя к углу. | |
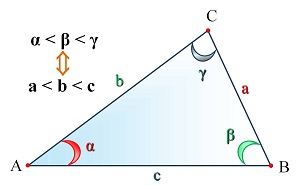
Точки - это вершины треугольника (обозначаются заглавными латинскими буквами - A, B, C). Отрезки - стороны треугольника (длины сторон обозначаются латинскими буквами - a, b, c). Обозначение сторон треугольника - AB, BC, AC. Величины углов противолежащие сторонам при соответственных вершинах - греческими буквами α, β, γ. | |
| |
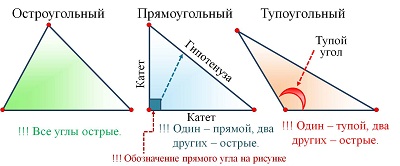
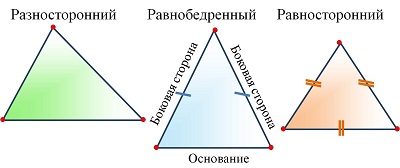
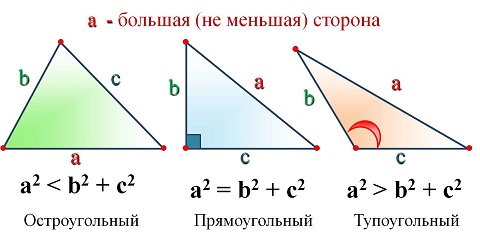
Треугольник называется прямоугольным, если у него есть прямой угол. Сторона, лежащая против прямого угла, называется гипотенузой. Стороны, между которыми прямой угол, называются катетами. Треугольник называется тупоугольным, если у него есть тупой угол. | Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называются боковыми сторонами. Третья сторона называется основанием. Треугольник называется равносторонним (правильным), если у него все стороны равны. |
|
|
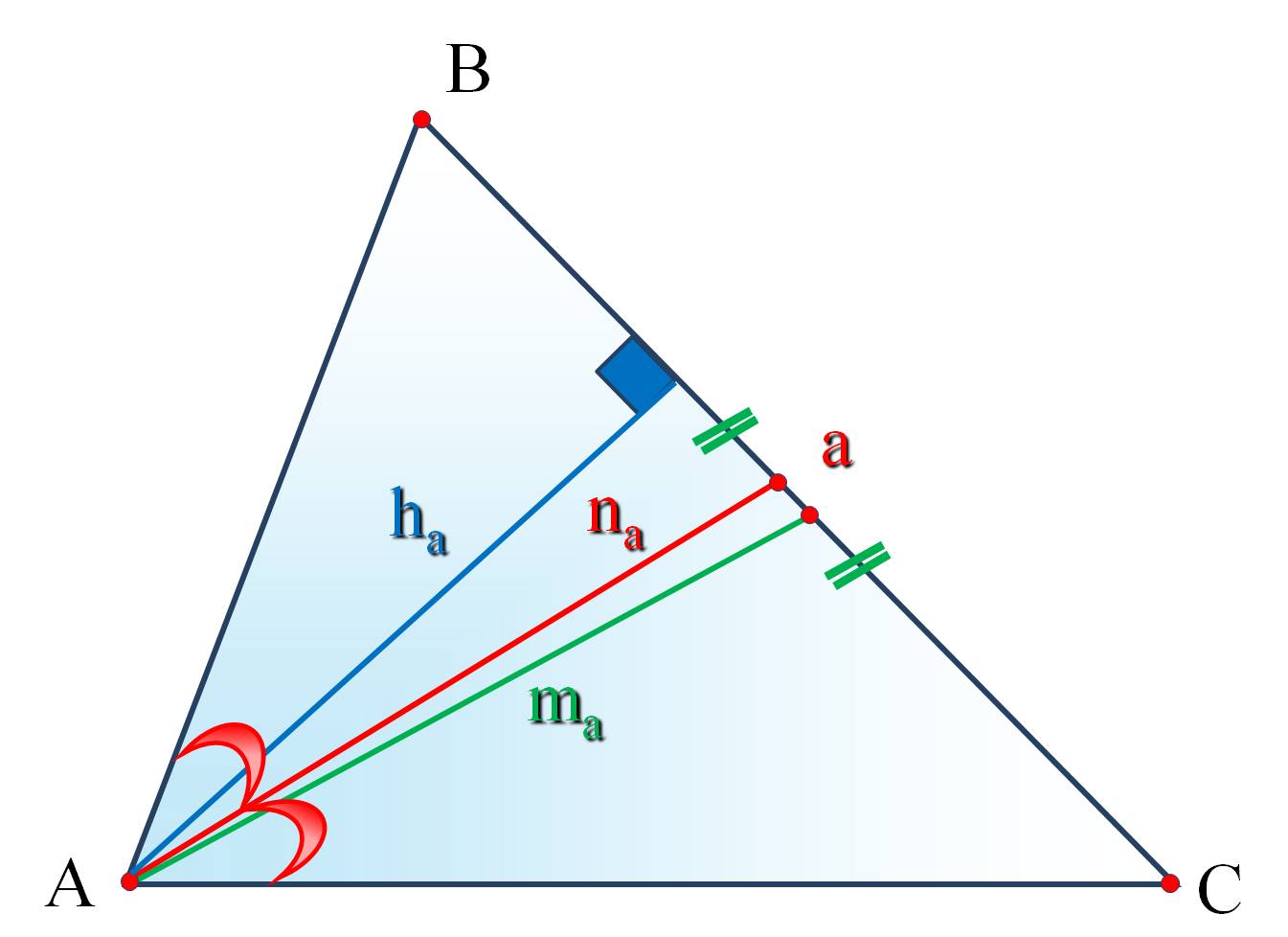
Опорные дидактические единицы: медиана; биссектриса; высота; средняя линия; серединный перпендикуляр. |
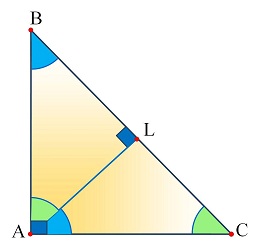
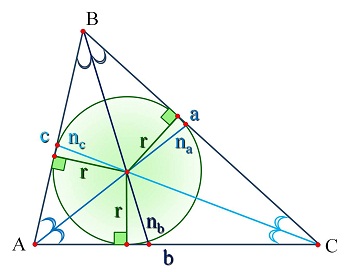
Биссектрисой треугольника называется называется отрезок биссектрисы любого угла от вершины до пересечения с противоположной стороной. Биссектрисой угла называется луч, исходящий из его вершины, проходящий между его сторонами и делящий данный угол пополам. Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Серединным перпендикуляром называется прямая, проведенная перпендикулярно к стороне треугольника через её середину. Обозначения: a, b, c - длины сторон треугольника; ma - медиана треугольника к стороне а; ha - высота треугольника к стороне а; na - биссектриса треугольника к стороне а. |
|
Опорные дидактические единицы: высота; точка пересечения высот треугольника или их продолжений; ортоцентр. | ||||||
Проведение высот в различных видах треугольников.
| ||||||
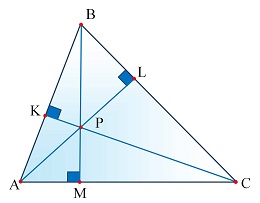
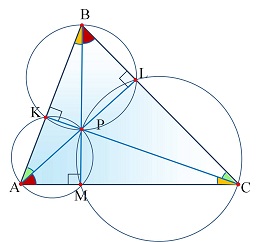
Полезные геометрические конструкции для решения сложных задач
|
Опорные дидактические единицы: медиана треугольника; центр масс треугольника; равновеликие треугольники. |
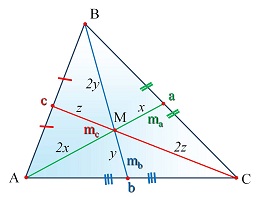
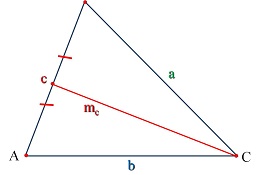
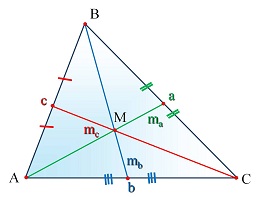 Медианой треугольника называется отрезок, соединяющий вершину угла треугольника с серединой противолежащей стороны. Медианой треугольника называется отрезок, соединяющий вершину угла треугольника с серединой противолежащей стороны.Обозначения: a, b, c - длины сторон треугольника; ma - медиана треугольника к стороне а; mb- медиана треугольника к стороне b; mc - медиана треугольника к стороне c. |
Эта точка всегда находится внутри треугольника и называется центром масс треугольника.
| Теорема. Медианы пересекаются в одной точке и делят треугольник на 6 равновеликих треугольника. Фигуры называются равновеликими, если их площади равны. 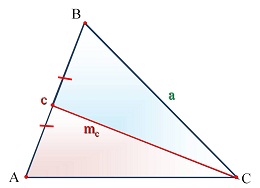 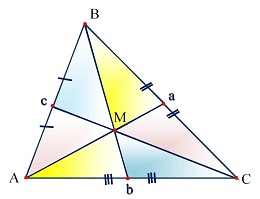 |
Формулы: | |
Опорные дидактические единицы: биссектриса угла; биссектриса угла треугольника; центр вписанной окружности; пропорциональные отрезки. | |
 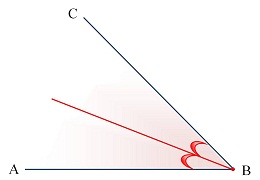 Биссектрисой угла называется луч, исходящий из его вершины, проходящий между его сторонами и делящий данный угол пополам. Биссектрисой угла называется луч, исходящий из его вершины, проходящий между его сторонами и делящий данный угол пополам. Биссектрисой треугольника называется отрезок, соединяющий вершину угла треугольника с серединой противолежащей стороны. Обозначения: a, b, c - длины сторон треугольника; na - биссектриса треугольника к стороне а; nb - биссектриса треугольника к стороне b; nc - биссектриса треугольника к стороне c. | |
Свойства биссектрис треугольника | |
Обратная теорема. Если точка равноудалена от сторон угла, то она лежит на биссектрисе этого угла.
| 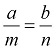 . . Теорема. Биссектриса треугольника делит сторону на части, пропорциональные прилежащим сторонам.
|
|
|
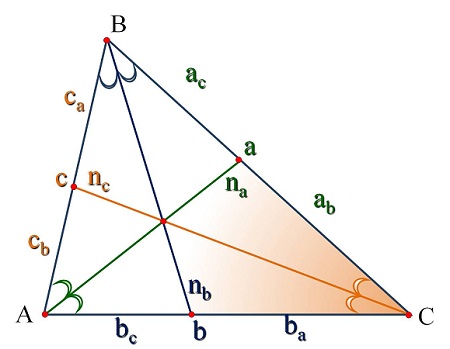 Формулы для вычисления бисссектрис: Формулы для вычисления бисссектрис: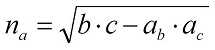 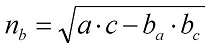 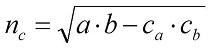 | |
Опорные дидактические единицы: средняя линия треугольника. | |
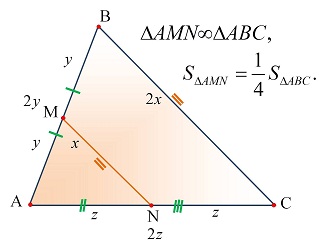
В любом треугольнике можно провести 3 средние линии. 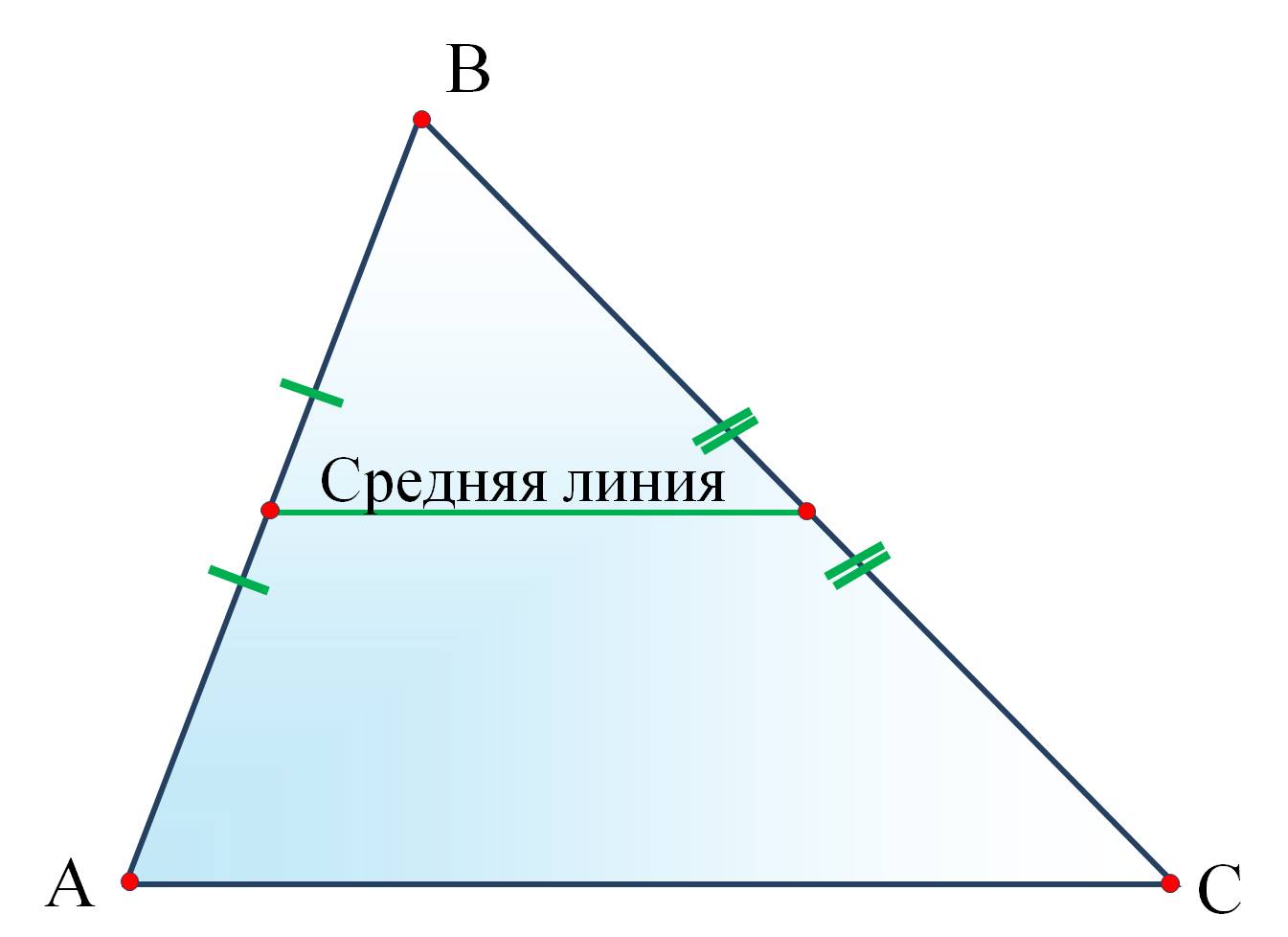 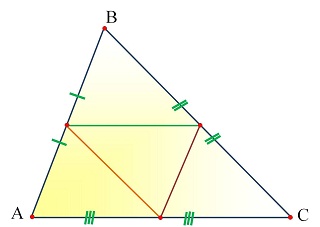 | Свойства средней линии треугольника. Теорема 1. Средняя линия треугольника параллельна третьей стороне и равна её половине. 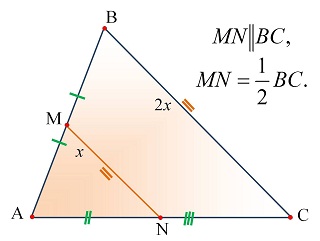 Теорема 2. Средняя линия треугольника отсекает от него треугольник, ему подобный, площадь которого составляет четверть от площади исходного.
|
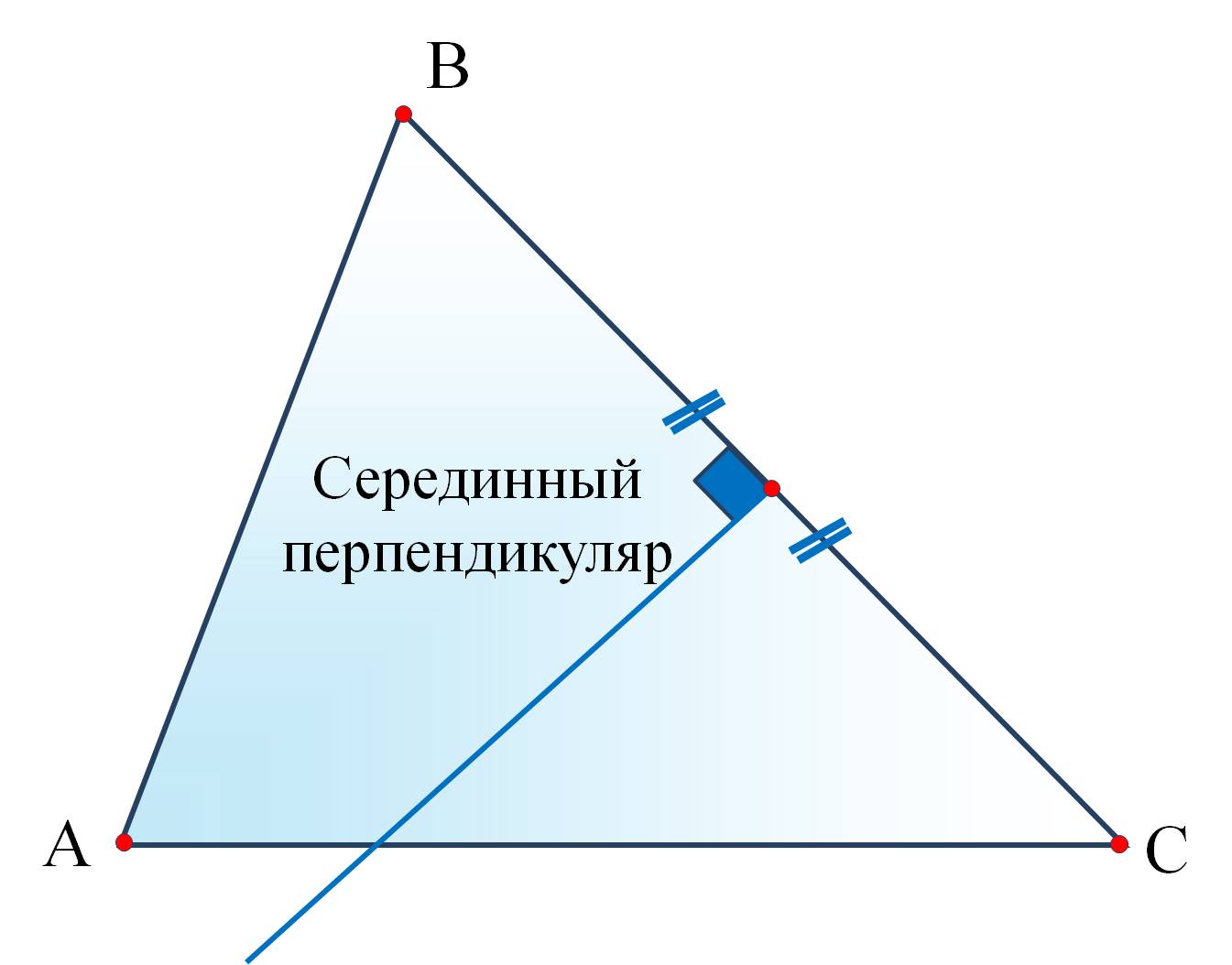
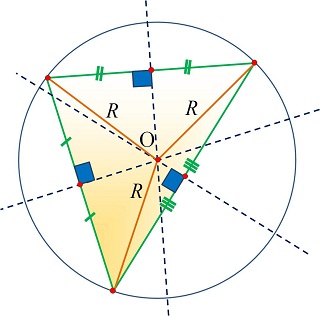
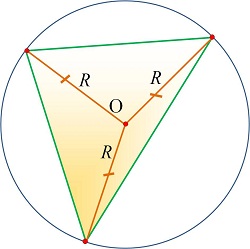
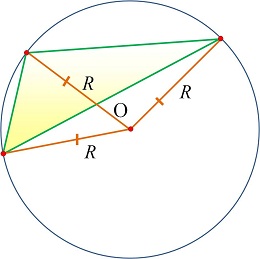
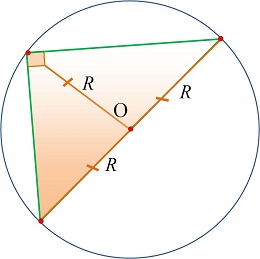
Опорные дидактические единицы: серединный перпендикуляр к отрезку; центр описанной окружности вокруг треугольника; точка пересечения серединных перпендикуляров. | ||||
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину. Теорема. Любая точка серединного перпендикуляра, проведённого к отрезку, равноудалена от его концов. Обратная теорема. Если точка плоскости равноудалена от концов отрезка, то она лежит на серединном перпендикуляре, проведённом к этому отрезку.
| Теорема. Три серединных перпендикуляра, проведённых к сторонам треугольника, пересекаются в одной точке. И эта точка называется центром описанной окружности вокруг треугольника.
| |||
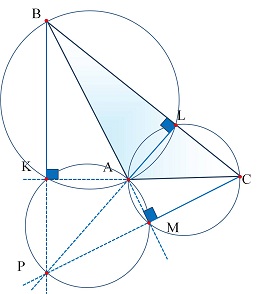
Замечательные геометрические конструкции, помогающие в решении задач | ||||
| ||||
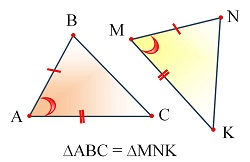
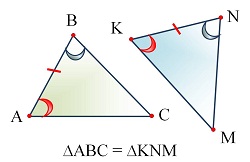
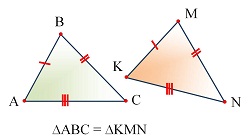
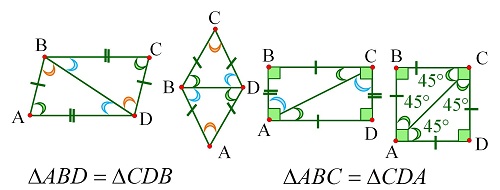
Опорные дидактические единицы: равные фигуры; равные треугольники; соответственные стороны и углы; признаки равенства треугольников. | |||
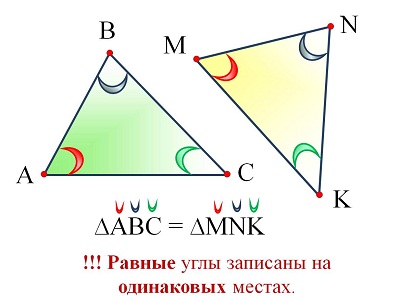 Фигуры называются равными, если их можно совместить наложением. Фигуры называются равными, если их можно совместить наложением. Треугольники называются равными, если их можно совместить наложением. Если треугольник АВС равен треугольнику MNK, то это означает, что элементы одного треугольника (углы, стороны) соответственно равны элементам другого треугольника. И записывают это так: ∆ABC = ∆MNK. Запись ∆ABC = ∆MNK означает, что АВ = MN, BC = NK, AC = MK. | |||
Признаки равенства треугольников
| |||
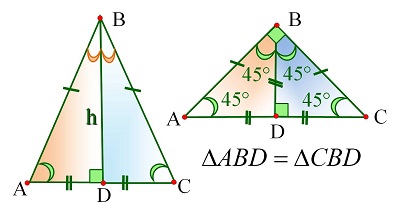
Свойства равных треугольников
| |||
Замечательные геометрические конструкции, помогающие в решении задач
|
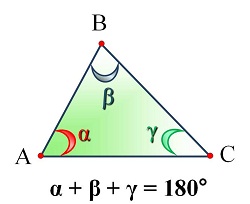
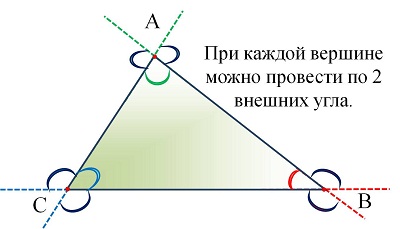
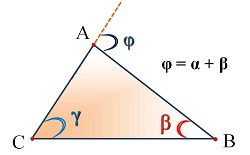
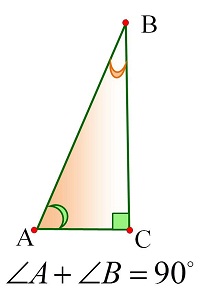
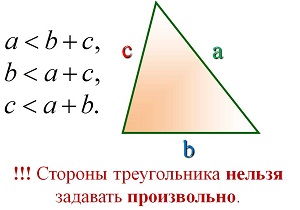
Опорные дидактические единицы: треугольник; внешний угол треугольника; сумма углов треугольника; неравенство треугольника. | |||
| |||
| |||
|
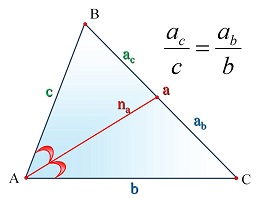
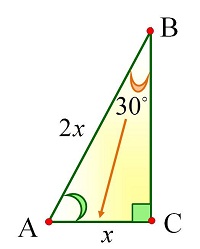
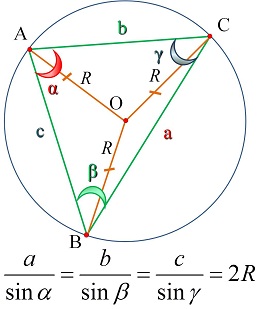
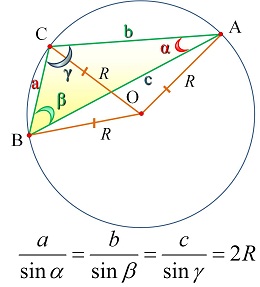
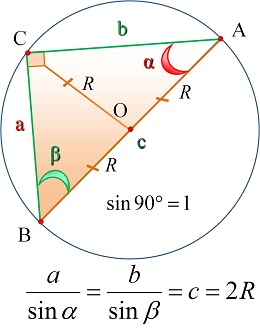
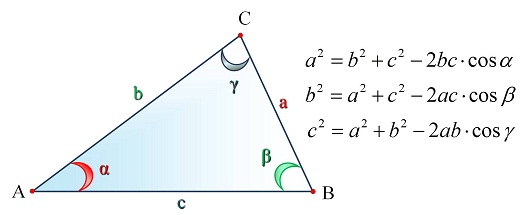
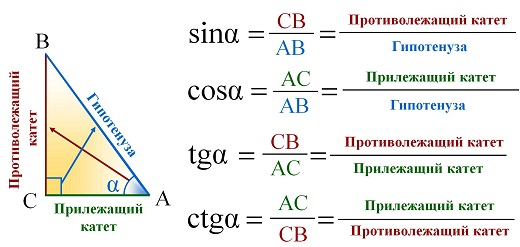
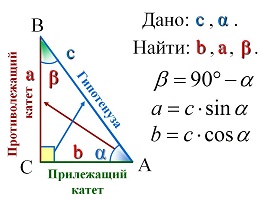
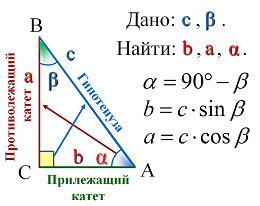
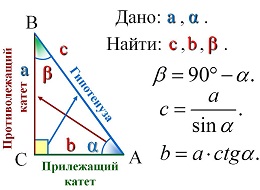
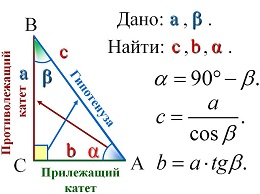
Опорные дидактические единицы: треугольник; радиус описанной окружности; теорема синусов; теорема косинусов; синус, косинус, тангенс острого угла прямоугольного треугольника; решение треугольников. | ||||||||||||||||||||
Теорема синусов
| ||||||||||||||||||||
Теорема косинусов
| ||||||||||||||||||||
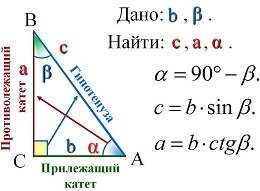
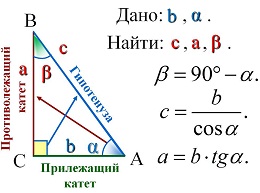
Решение прямоугольных треугольников
| ||||||||||||||||||||